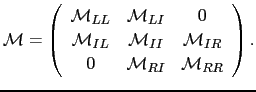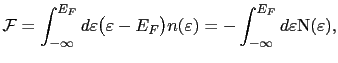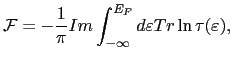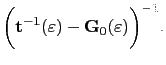The Korringa-Kohn-Rostoker (KKR) method was developed initially by Korringa in 1947 [148] who used the multiple-scattering theory to solve the Schrödinger equation and determine the band structure of a periodic solid. Seven years later Kohn and Rostoker [149] proposed a method equivalent to the Korringa one but using Green's functions, called in our days the Korringa-Kohn-Rostoker (KKR) method. Perhaps the most important characteristic of the KKR method is that its formal structure does not change when going from non-relativistic to relativistic description.
The KKR method has undergone several improvements since the late forties. One of these improvements is the so-called screened Korringa-Kohn-Rostoker (SKKR) method. The SKKR method allows to calculate the electronic properties of surface, interface and in general layered systems with periodicity only in two dimensions, within the frame work of multiple-scattering theory without any further approximations.
In multiple scattering theory the scattering path operator (
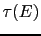 ) from which the Green function and electronic properties are calculated, is given in terms of the structure constant
) from which the Green function and electronic properties are calculated, is given in terms of the structure constant
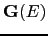 , and the single-site scattering matrix
, and the single-site scattering matrix
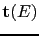 :
:
![$\displaystyle \mathbf{\tau}(E)=\biggl[\mathbf{t}^{-1}(E)-\mathbf{G}(E)\biggr]^{-1}.$](img794.gif) |
(88) |
2D periodicity leads in principle to infinite matrix. However, the screening method allows to transform
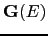 to the screened structure constants, which have spatial short-range. In general the screening results in the fact that layers interact only up to a certain number of neighboring layers.
For a layered structure it is convenient to divide the parent lattice in three regions, a left semi-infinite system (L), a right semi-infinite (R), and an intermediate interface region, the properties of which to be calculated. This formal partitioning of the parent infinite system implies that the inverse of the scattering path operator
to the screened structure constants, which have spatial short-range. In general the screening results in the fact that layers interact only up to a certain number of neighboring layers.
For a layered structure it is convenient to divide the parent lattice in three regions, a left semi-infinite system (L), a right semi-infinite (R), and an intermediate interface region, the properties of which to be calculated. This formal partitioning of the parent infinite system implies that the inverse of the scattering path operator
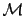 also has the form [150]:
also has the form [150]:
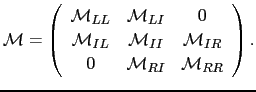 |
(89) |
This shape is a direct consequence of the short-range of the structure constant. Using the concept of principal layer [151], which is defined so that it interacts only with nearest-neighbors principal layers, one can rewrite the structure constants, and consequently the inverse of the scattering path operators, in tridiagonal form. From them the Green function of the system can be calculated from a decimation technique [152,153].
The free energy derived in the frame work of the fully relativistic SKKR method at zero temperature is approximated by:
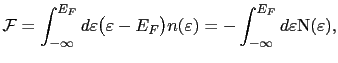 |
(90) |
where 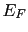 is the Fermi energy of the system,
is the Fermi energy of the system,
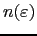 is the density of states (DOS), and
is the density of states (DOS), and
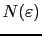 is the integrated density of states. Using the Lloyd's formula [154], the free energy can be written as follow:
is the integrated density of states. Using the Lloyd's formula [154], the free energy can be written as follow:
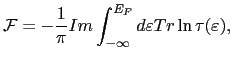 |
(91) |
where
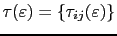 is the site-angular momentum representation of the scattering path operator, which can be expressed as a function of the site-diagonal single scattering matrix
is the site-angular momentum representation of the scattering path operator, which can be expressed as a function of the site-diagonal single scattering matrix
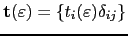 and the structure constants
and the structure constants
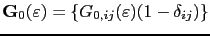 , in the following way:
, in the following way:
Rocio Yanes
![]() ) from which the Green function and electronic properties are calculated, is given in terms of the structure constant
) from which the Green function and electronic properties are calculated, is given in terms of the structure constant
![]() , and the single-site scattering matrix
, and the single-site scattering matrix
![]() :
:
![$\displaystyle \mathbf{\tau}(E)=\biggl[\mathbf{t}^{-1}(E)-\mathbf{G}(E)\biggr]^{-1}.$](img794.gif)