2 Kohn-Sham scheme

The electron density corresponding to the ground state can be calculated using a variational principle, we know that every 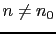$n\neq n_{0}$ has $E[n]>E_{0}=E[n_{0}]$. In this way Kohn and Sham added a tremendous addendum in 1965 [144], within their variational scheme an auxiliary system of non-interacting electrons is introduced. It is assumed that the ground state density of this hypothetical non-interacting electrons system is the same as that of the original interacting system.

In addition, the Kohn-Sham approach to the interacting electrons problem is to rewrite the Hohenberg-Kohn expression for the energy functional corresponding to the ground state as follows:

$$E_{KS} = T_{NI}[n]+E_{ext}[n] + E_{H}[n]+E_{xc}[n],$$ (79)

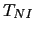where $T_{NI}$ is the kinetic energy of the non-interacting electron system. 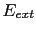$E_{ext}$ is the energy due to the external potential (external potential means that it is due to the atomic nuclei), and it has the following form:

$$E_{ext}[n] = \int d^{3}r V_{ext}(\vec{r})n(\vec{r}),$$ (80)

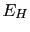$E_{H}$ is the Hartree energy, which can be expressed as a functional of the electron density of the system as follows:

$$E_{H}[n] = -\frac{e^{2}}{2}\int d^{3}r\int d^{3}(\vec{r'}) \frac{n(\vec{r})n(\vec{r'})}{\mid \vec{r} - \vec{r'}\mid},$$ (81)

and finally, 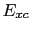$E_{xc}$ is the so called exchange correlation energy term which includes "all remaining" contributions.

We have to note that in practice the correct 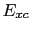$E_{xc}$ term is unknown, for this reason the determination of such functional requires some approximation, and it is this approximation which determines the accuracy of the method.