Next: 2 Free energy and Up: 2 The constrained Monte Previous: 2 The constrained Monte Contents
An ordinary Monte Carlo (MC) algorithm is widely used to compute thermodynamic properties by averaging over the Boltzmann distribution using the Metropolis
algorithm [123]. The Metropolis algorithm works by generating trial moves at random and accepting or rejecting each move based on the Boltzman probability density
![]() , where
, where
![]() (
(
![]() is the Boltzamn constant and T is the temperature).
The ratio
is the Boltzamn constant and T is the temperature).
The ratio
![]() depends on the energy difference between two states,
depends on the energy difference between two states,
![]() (
(
![]() is the Hamiltonian of the system).
In the usual Monte Carlo method for magnetic systems we generate our trial moves by
drawing a vector
is the Hamiltonian of the system).
In the usual Monte Carlo method for magnetic systems we generate our trial moves by
drawing a vector
![]() from an isotropic
normal distribution, choosing a spin
from an isotropic
normal distribution, choosing a spin
![]() at random,
adding
at random,
adding
![]() to it and normalizing the result
to obtain a trial spin
to it and normalizing the result
to obtain a trial spin
![]() .
.
The probability density of the move depends only on the angle
between
![]() and
and
![]() , which ensures reversibility.
The variance of the
, which ensures reversibility.
The variance of the
![]() distribution controls the average
step size and can be chosen at will
to improve the ratio of accepted to rejected moves,
similarly to the MC angle in Refs. [123,124].
For our Hamiltonian,
the energy difference involves only spin
distribution controls the average
step size and can be chosen at will
to improve the ratio of accepted to rejected moves,
similarly to the MC angle in Refs. [123,124].
For our Hamiltonian,
the energy difference involves only spin ![]() and
few neighboring spins to which it is coupled by exchange interaction,
so that the decision to accept or reject the move can be made quickly.
A sequence of
and
few neighboring spins to which it is coupled by exchange interaction,
so that the decision to accept or reject the move can be made quickly.
A sequence of ![]() moves, counting null moves, constitutes a sweep (or one Monte Carlo step);
we compute quantities of interest once per sweep to average them.
moves, counting null moves, constitutes a sweep (or one Monte Carlo step);
we compute quantities of interest once per sweep to average them.
The constrained Monte Carlo method has been suggested by P. Asselin from Seagate technology [125,126] in relation to the necessity to model high temperature spin dynamics in the heat-assisted magnetic recording. The innovation of the constrained Monte Carlo method is to modify the elementary steps of the random walk so as to conserve the average magnetization direction
![]() .
In this way we sample the Boltzmann distribution
over a submanifold of the full phase space.
Thus we keep the system out of thermodynamic equilibrium in a
controlled manner, while allowing its microscopic degrees of freedom
to thermalize.
.
In this way we sample the Boltzmann distribution
over a submanifold of the full phase space.
Thus we keep the system out of thermodynamic equilibrium in a
controlled manner, while allowing its microscopic degrees of freedom
to thermalize.
In the constrained Monte Carlo method the trial moves
act on two spins at a time.
The extra degrees of freedom allow us to fix
![]() to any given unit
vector, which we take here to be the positive
to any given unit
vector, which we take here to be the positive ![]() axis since we can always
reduce the problem to this case by means of a global rotation.
In detail, the algorithm is the following:
axis since we can always
reduce the problem to this case by means of a global rotation.
In detail, the algorithm is the following:
| (57) | ||
| (58) |
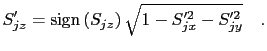 |
(59) |
| (60) |
![$\displaystyle P=\min\Biggl[1, \biggl(\frac{M_z'}{M_z}\biggr)^2 \frac{\lvert S_{...
...{\lvert S_{jz}'\rvert } \exp\bigl(-\beta\Delta \mathcal{H}\bigr) \Biggr] \quad.$](img592.gif) |
(61) |
In effect, we use the compensation spin to project the system back to its admissible manifold. The projection is not orthogonal and does not preserve measure. Consequently the Boltzmann ratio in step 7 is multiplied by a geometric correction, the ratio of two Jacobians (derived in details in Ref. [126]). The reversibility and the ergodicity of this new Monte Carlo method have been rigorously proved, see Ref. [126].
Rocio Yanes