Next: 2 First-order surface-anisotropy energy Up: 3 Analytical background Previous: 3 Analytical background Contents
| (25) |
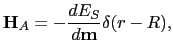 |
(26) |
For the case of ![]() we can suppose that the deviations of
we can suppose that the deviations of
![]() of the homogeneous state
of the homogeneous state
![]() are small and the problem can be linearized.
are small and the problem can be linearized.
| (27) |
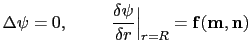 |
(28) |
![$\displaystyle \mathbf{f(m,n)}=-\frac{1}{J}\Bigl[\frac{dE_{S}(\mathbf{m_{0},r})}...
...S}(\mathbf{m_{0},r})}{d\mathbf{m}}\cdot\mathbf{m_{0}}\Bigr)\mathbf{m_{0}}\Bigr]$](img304.gif) |
(29) |
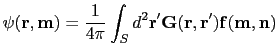 |
(30) |
The equation (2.15) was obtained analytically for
![]() in the range of the particle size large enough (
in the range of the particle size large enough (
![]() ) but small enough so that
) but small enough so that
![]() remains small. Being
remains small. Being
![]() , the angle of order which describes the noncollinearity of the spins that results from the competition of the exchange interaction and the surface anisotropy
, the angle of order which describes the noncollinearity of the spins that results from the competition of the exchange interaction and the surface anisotropy ![[*]](footnote.gif) .
.
Since ![]() is nearly size independent (i.e. the whole energy of the particle scales with the volume), it is difficult to experimentally distinguish between the core cubic anisotropy and the one due to the second order surface contribution (see discussion later on). The physical reason for the independence of
is nearly size independent (i.e. the whole energy of the particle scales with the volume), it is difficult to experimentally distinguish between the core cubic anisotropy and the one due to the second order surface contribution (see discussion later on). The physical reason for the independence of ![]() on the system size is the deep penetration of the spin non-collinearities into the core of the particle. This means that the angular dependence of the non-collinearities also contributes to the effective anisotropy. Interestingly this implies that the influence of the surface anisotropy on the overall effective anisotropy is not an isolated surface phenomena and is dependent on the magnetic state of the particle. We note that this effect is quenched by the presence of the core anisotropy which could screen the effect at a distance of the order of domain wall width from the surface.
on the system size is the deep penetration of the spin non-collinearities into the core of the particle. This means that the angular dependence of the non-collinearities also contributes to the effective anisotropy. Interestingly this implies that the influence of the surface anisotropy on the overall effective anisotropy is not an isolated surface phenomena and is dependent on the magnetic state of the particle. We note that this effect is quenched by the presence of the core anisotropy which could screen the effect at a distance of the order of domain wall width from the surface.
The energy contribution
![]() has also been derived in the presence of core anisotropy [73] and numerically tested in Ref. [87].
Similar conclusions also apply for the case of the transverse surface anisotropy, Ref. [87].
has also been derived in the presence of core anisotropy [73] and numerically tested in Ref. [87].
Similar conclusions also apply for the case of the transverse surface anisotropy, Ref. [87].
Rocio Yanes